Measure the Earth on March 21, 2023!
- Discover the Universe

- Feb 27, 2023
- 4 min read
Updated: Aug 1, 2024
The Earth will pass through the spring equinox on March 21, 2023, which provides an excellent opportunity to measure the circumference of the Earth with your students. Use a stick and ruler to replicate an ancient experiment and bring a big concept to a direct, hands-on experience. This activity will help your students find connections between their skills and learning in math, astronomy, history, and geography.

With simple observations and geometry, Eratosthenes took advantage of the unique orientation of the Earth and Sun and measured the circumference of the Earth to amazing accuracy over 2200 years ago. Eratosthenes was a Greek astronomer, geographer, mathematician, philosopher, and more - a master of all trades at the time. He lived from 276 BC to 194 BC and was the chief librarian of the Library of Alexandria.
Eratosthenes noticed that during times of the year when the Sun was directly overhead in Syene, now known as Aswan, it would light up the bottom of wells and no shadows were cast. At the same time, however, shadows were still cast in Alexandria, slightly north of Syene. When the Sun was at local noon and directly overhead in Syene, he measured the angle of the shadow cast from a monolith in Alexandria. Knowing the distance between Syene and Alexandria, he could then use simple geometry to estimate the circumference of the Earth. With his measurements at the time, he calculated the circumference of the Earth to be 40,000 km, only 75 km off from the true circumference. That’s over 99% accurate!
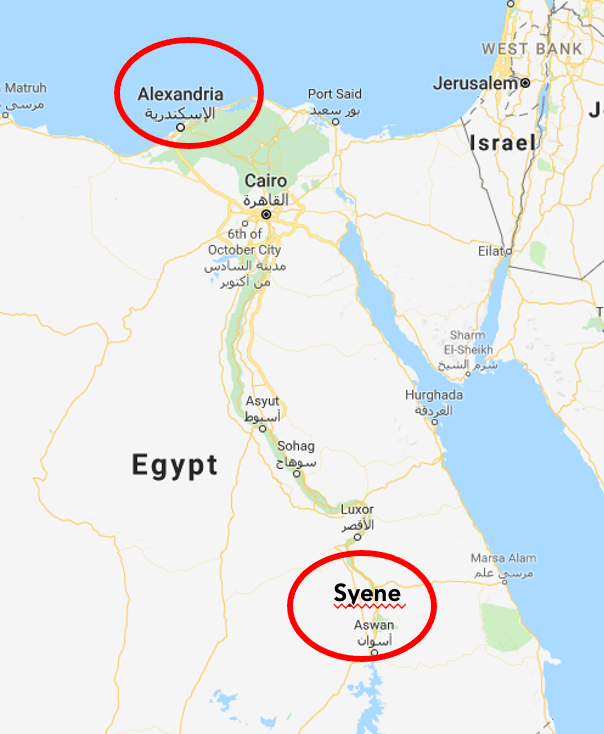 Credit: Adapted from Google Maps |  Credit: ASTROLab du Mont-Mégantic |
|---|
We can still replicate Eratosthenes’ experiment today, and measure the circumference of the Earth for ourselves. The best time to do this measurement is during the equinox. On the equinox, the Sun is directly overhead at the equator and the Sun’s rays hit the ground at a 90º angle. This only happens twice a year, on the spring and fall equinoxes. To participate in this experiment for the upcoming equinox, select a stick of known length, such as a metre stick, and have a ruler or measuring tape handy. Then complete the following steps.
Find the time of local noon on the equinox at your location (when the Sun will be at its highest point).
You can find this information by using Stellarium or the NOAA Solar Calculator.

Measure the shadow of your stick at local noon on the equinox.
Place your stick vertically such that one end is on the ground and its length is perpendicular to the ground. Measure the length of the shadow cast by the stick using your ruler or measuring tape.

Calculate the angle Formed by the shadow.
Knowing the length of the stick and the length of the shadow gives you two sides of a right triangle. You can use trigonometry to find the angle formed by the shadow, plug your stick and shadow length into our excel sheet, or draw the triangle to scale and measure the angle with a protractor.
Collaborate with another school at a similar longitude OR use the data for an imaginary school on the equator.
Just like Eratosthenes, you will need measurements from two locations to calculate the circumference of the Earth.
Experiments are always more fun with partners, and you can join the International Eratosthenes Experiment to partner with another school. The deadline to register is March 17, 2023.
You can also find your own partners to work with. A partnering school should be directly North or South of you and at least 65 km away. Schools that are closer together are more likely to have the same measurement, and less likely to have a meaningful result.
If you would prefer to work with just your students or aren’t able to find another school to work with, you can use information from an imaginary school located on the equator that is at the same longitude as your location. In this case, the imaginary school’s angle is 0º as their stick wouldn’t cast a shadow.
Whether you are partnering with a real or imaginary school, you will need to find the distance between your location and theirs. You can find the distances between two locations using the National Geographic MapMaker as well as Google Earth.
Calculate the circumference of the Earth.
With the angle measured at your school, the other school, and the distance between each school, you have all the information needed to define an arc on the Earth. You can then use geometry to compare the arc you have measured with the full circumference of the Earth.
 Credit: ASTROLab du Mont-Mégantic |  Credit: Eratosthenes Experiment |
The angle made by the shadows at each of your school’s location is the same angle that the Sun’s rays are making at your location. During the equinox, this angle describes the angle of the arc between your school and the equator. When combined with the information from another school, the difference in the angles defines the arc between your schools, as shown in the image above.
You can now compare the arc between your school and your partner school with the circumference of the earth using like ratios. The difference in angles between your schools over 360º is the same as the distance between your schools over the total circumference of the Earth. So, the Earth’s circumference can be found by multiplying 360º by the distance between your schools and then dividing by the difference in the angles you measured. Note that if you and your partner school are on opposite sides of the equator, say you are in the Northern Hemisphere and your partner school is in the Southern hemisphere, you will sum your measured angles instead.
If you want to use less math, you can use our excel sheet to calculate the circumference of the Earth directly from your measurements.
We hope you enjoy measuring the Earth with your students and making meaningful partnerships with schools around the world!
For more information about the Eratosthenes Experiment and the steps we have laid out here, check out our recorded webinar and slides:
Webinar: Measure the Earth with your Students (YouTube video, 59 minutes)
Please reach out to CJ at charles@discovertheuniverse.ca for any questions you have about this experiment and content showcased here.



